⏳Время прочтения: 5 минут
Введение
При подготовке тематических карт, таких как хороплеты, вы неизбежно столкнетесь с тем, что вам придется решить, каким образом покрасить объекты на вашей карте. Эта статья стремится помочь вам сделать наилучший выбор и ответить на некоторые вопросы.

То, как мы красим страны на карте Южной Америки, влияет на восприятие, какие страны нам кажутся беднее, а какие богаче. Например, с помощью классификации данных, используя один и тот же датасет, мы можем немного обмануть читателя и показать Боливию (самая бедная на карте слева) чуть богаче соседей, чем она есть на самом деле.
Зачем классифицируют данные и на что это влияет
Задача классификации данных состоит в том, чтобы распределить числовую выборку на группы таким образом, чтобы наиболее репрезентативно представить распределение явлений, представленных нашей числовой выборкой. Важно не просто показать большие и маленькие значения, но и значимые промежуточные группы, если таковые есть.
Существует множество методов классификации данных. Иногда лучше это сделать вручную, а иногда лучше и гораздо быстрее использовать один из стандартных методов.
Наиболее часто используемые алгоритмы классификации:
- равные интервалы;
- естественные интервалы (алгоритм Дженкса);
- квантили;
- стандартное отклонение;
- логарифмическая шкала.
Как работает каждый из алгоритмов и какие у них плюсы и минусы, продемонстрируем на карте плотности населения в Южной Корее, которую вы могли видеть в нашей статье про карты-анаморфозы.
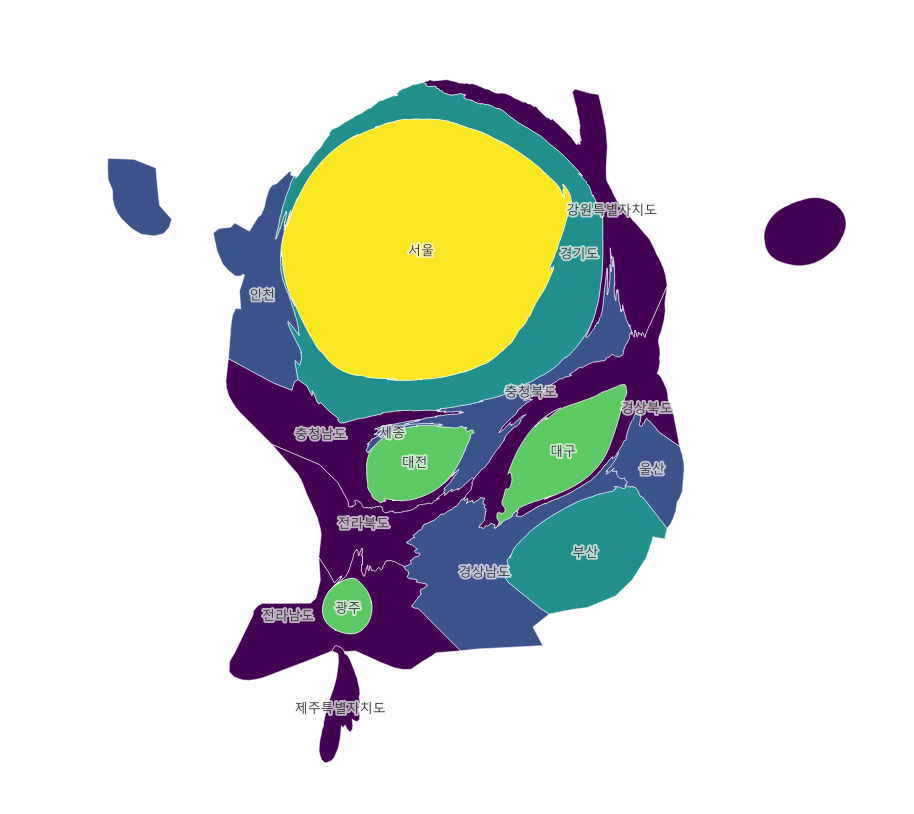
Равные интервалы
Алгоритм "Равные интервалы" делит данные на классы равного размера, например: от 0 до 100, от 100 до 200 и т.д. Он отлично подходит, когда данные равномерно распределены, и выглядит очень понятно, если показывать процентные данные. Но он плохо подходит, если есть значения, которые удалены от основной массы чисел, это приводит к созданию лишних пустых интервалов.
Математика алгоритма очень проста. Из максимального значения вычитается минимальное, и полученная разность делится на количество нужных нам интервалов.
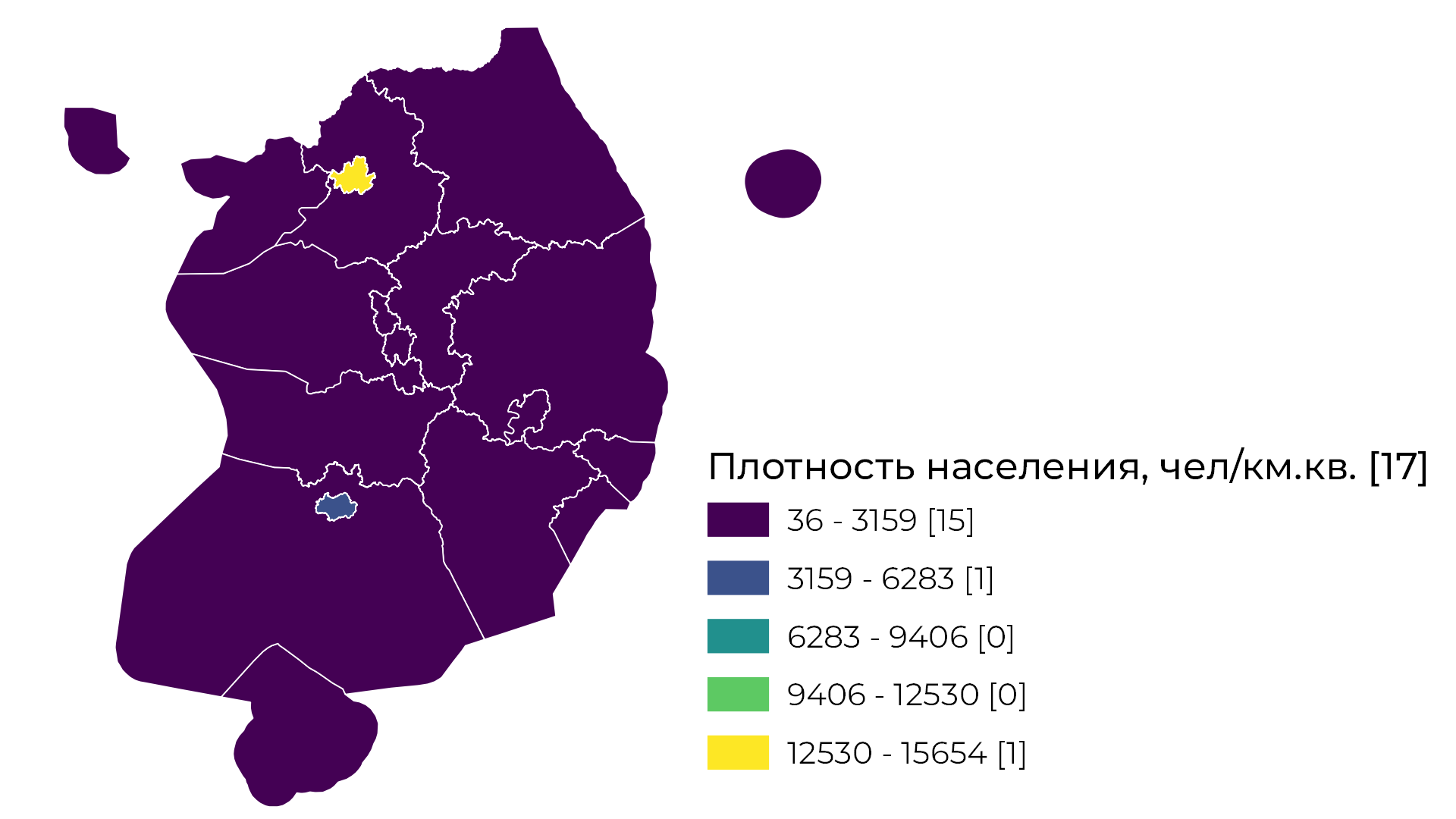
Естественные интервалы (алгоритм Дженкса)
Естественные интервалы – отличный алгоритм, который подходит ко множеству задач классификации. Он разбивает значения на классы таким образом, чтобы схожие значения оказались в одном классе. Объекты разделены на классы, границы которых установлены там, где существуют относительно большие различия в значениях данных.
В связи с этим способ естественных интервалов можно использовать почти для любой задачи классификации, собственно, многие буквально так и делают. Так как каждый набор данных дает свое уникальное решение по классификации, метод не подходит в ситуациях, если нужно сравнить данные об одной территории за разные года.
С математической точки зрения алгоритм работает так:
а) рассчитывается сумма квадратов отклонений всех значений нашей выборки от среднего арифметического этой выборки;
б) выборка разбивается множеством способов на заданное количество классов. Для каждого класса рассчитывается среднее арифметическое и сумма квадратов отклонений от этого среднего арифметического. После чего суммы квадратов отклонений от среднего для каждого класса складываются. Действие повторяется для каждого способа разделения на классы;
в) определяется лучший вариант классификации путем сравнения того, что получилось в пунктах а и б по формуле (а - б) / а. Тот способ разделения на классы, который дает результат ближе всего к единице, становится результатом работы алгоритма.
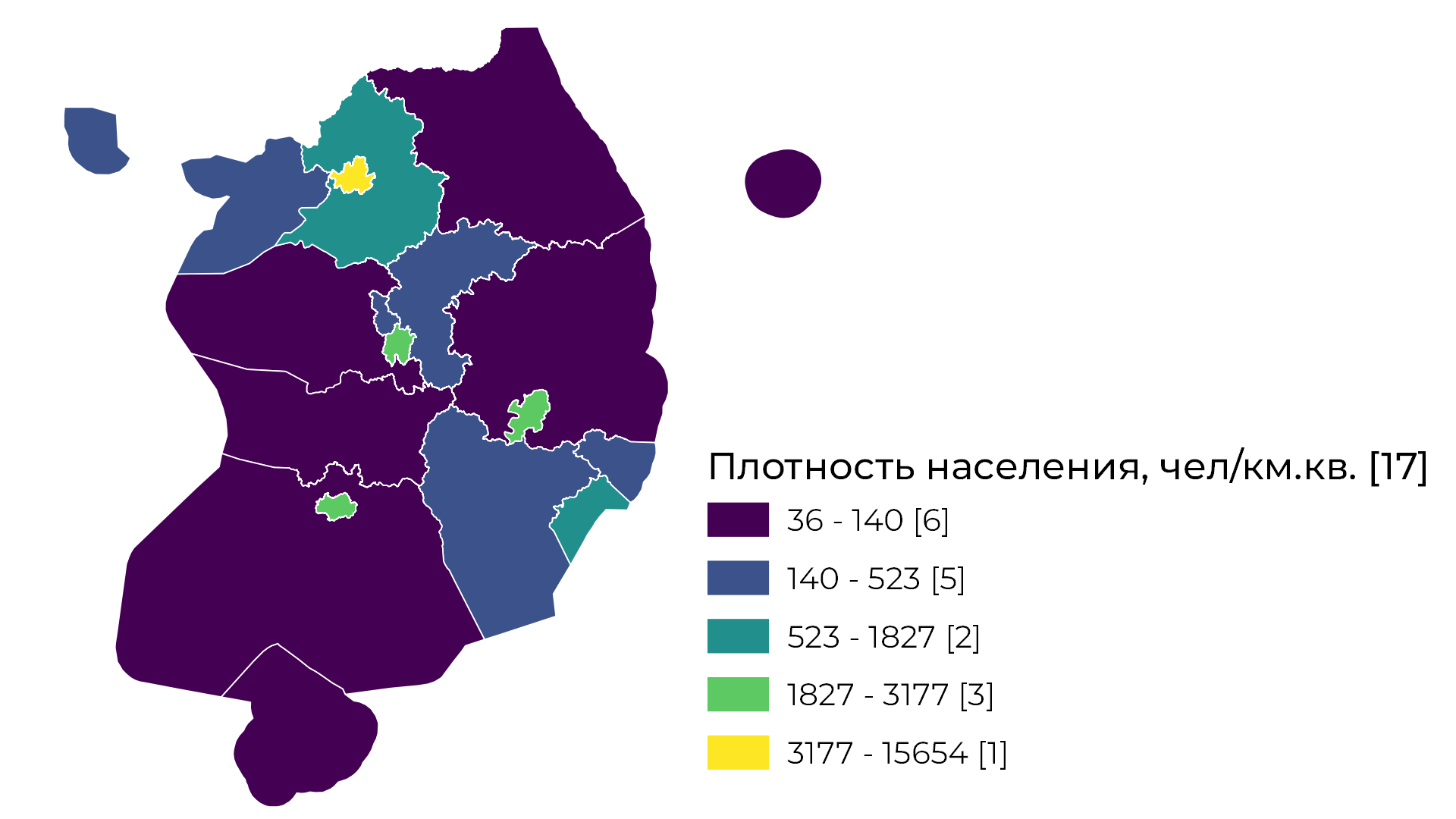
Квантили
Все очень просто, алгоритм делит данные на классы таким образом, чтобы в каждом классе было одинаковое или наиболее близкое к одинаковому количеству чисел. Главный минус метода в том, что одинаковые значения могут оказаться в разных классах, что можно частично решить путем увеличения количества классов.
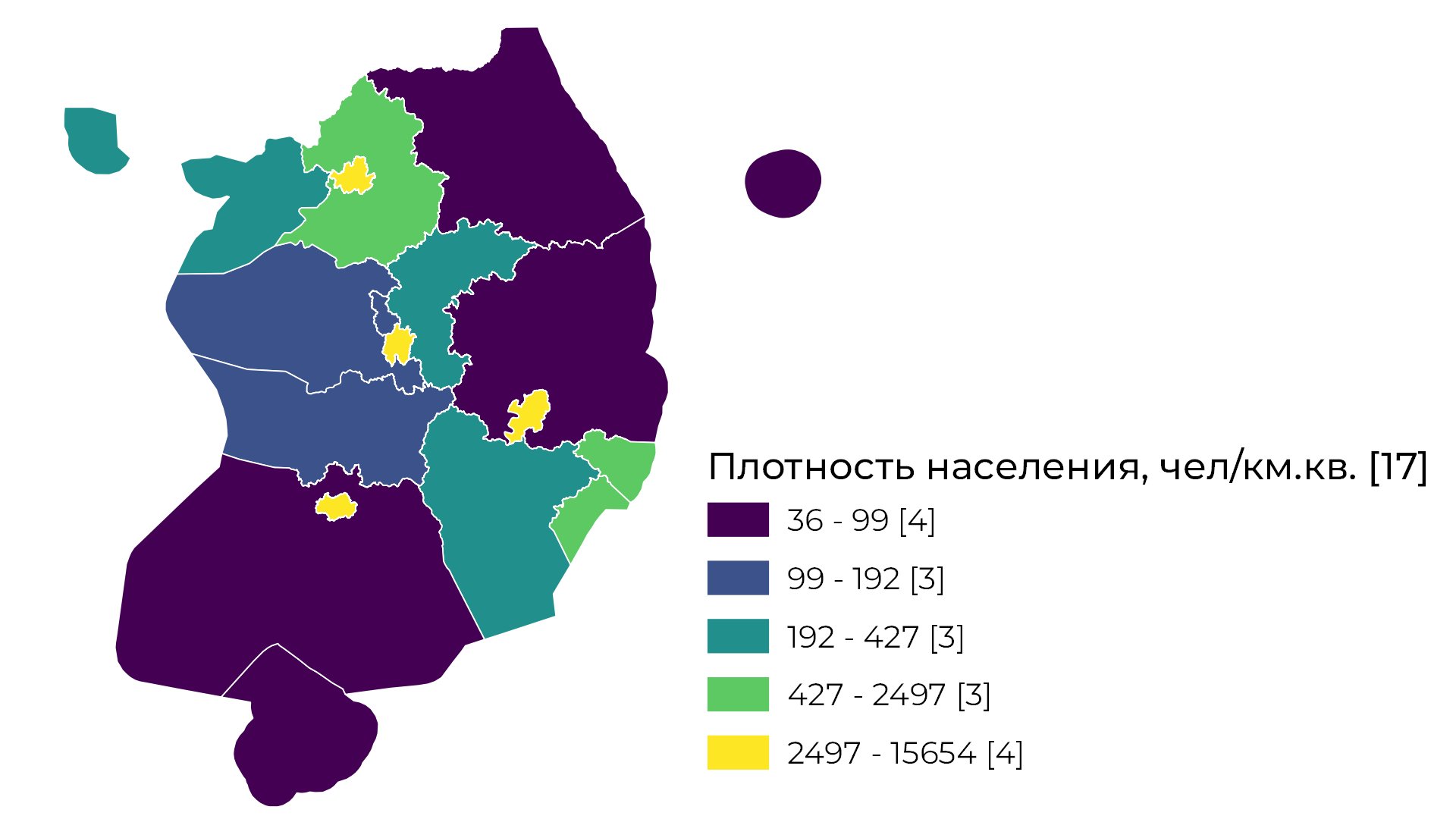
Стандартное отклонение
Метод классификации стандартных отклонений показывает, насколько число отличается от среднего значения выборки. Разрывы классов создаются с равными диапазонами значений, пропорциональными стандартному отклонению — обычно с интервалами в единицу, половину, одну треть или одну четверть — с использованием средних значений и стандартных отклонений от среднего значения. Метод подходит, если значения выборки распределены так, что это похоже на нормальное распределение.
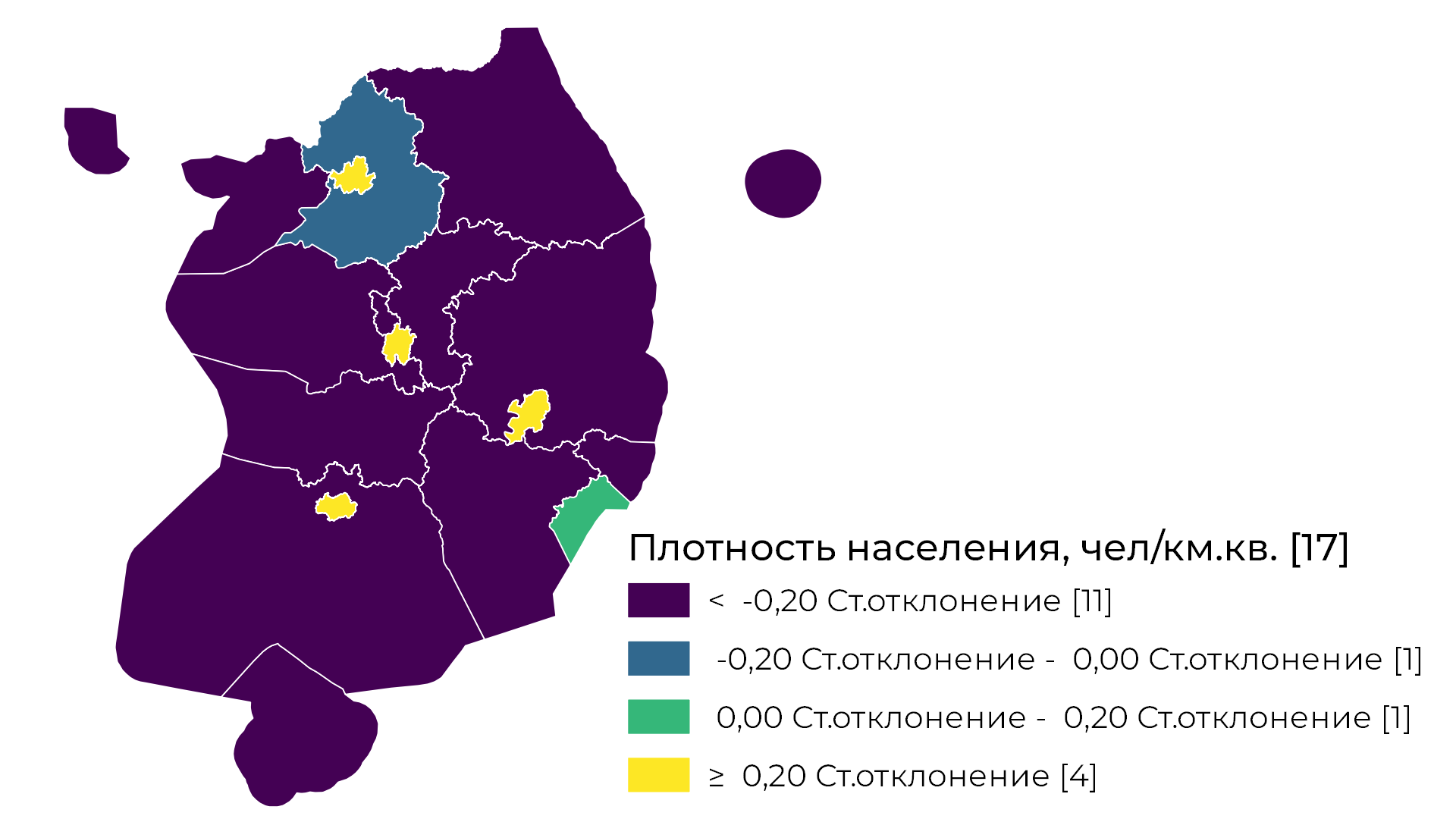
Логарифмическая шкала
Этот метод концептуально похож на равные интервалы и стандартное отклонение. Выборка разбивается на классы таким образом, чтобы границей класса было число, возведенное в определенную степень. В нем есть все наши любимые минусы с неравномерным распределением значений по классам и с возможностью создания пустых классов. Подходит в ситуациях, когда нужно показать, во сколько раз в одном месте значения больше чем в другом, но карты получаются не самыми легкими для восприятия.

Ручной метод
Алгоритмы серьезно ускоряют время подготовки карт, некоторые можно использовать часто или почти всегда, как естественные интервалы, а есть и весьма специфические. Но прежде чем использовать один из алгоритмов, не забывайте задать себе один из следующих вопросов, на который сможете ответить только вы, а не одно из этих математических творений человечества:
- Есть ли важные границы данных, которые необходимо «встроить» в классификацию?
- Должна ли одна из границ класса быть средним арифметическим, медианой или модой числа?
- Является ли эта карта частью серии, которой нужны одни и те же классы на всех картах для сравнения?
Часто погружение в контекст данных подскажет, что лучше разбить выборку на классы вручную, например, в ситуациях, когда нужно использовать какие-либо нормативные значения или когда можно обойтись всего двумя классами, как в примере со сравнением отношения численности овец и людей по странам:

Источники
Материал подготовил Александр Зуев
