Статьи

Интерполяция в QGIS, часть 1

2023-08-23 18:17 ГИС Туториалы
Время прочтения: 6 минут

Введение

На протяжении всей истории картографии одной из важнейших проблем было выявление информации о неизвестном на основании известного. Даже при предполагаемых (очень неточных) вводных это было частью механизма принятия решений, который приводил к большим тратам и к большим доходам. Карты древности строились на основании всего лишь нескольких известных координат и рассказов путешественников, которые опускали часть про огромные километры пространства, скрывающиеся между несколькими наиболее примечательными точками.
Предположение древнегреческих ученых о сферической природе нашей планеты и возможности ее обогнуть и приплыть к Индии с другой стороны стали основанием для вложения больших денег во множество экспедиций, в том числе и Христофора Колумба [История географических карт. Ллойд Арнольд Браун].
Источник - https://ru.wikipedia.org/wiki/География_(Птолемей)#/media/Файл:PtolemyWorldMap.jpg
Покупка Луизианы Америкой строилась на основании предположения о расположении истока реки Миссисипи, когда он еще не был найден, что также влияло на стоимость такой огромной территории.
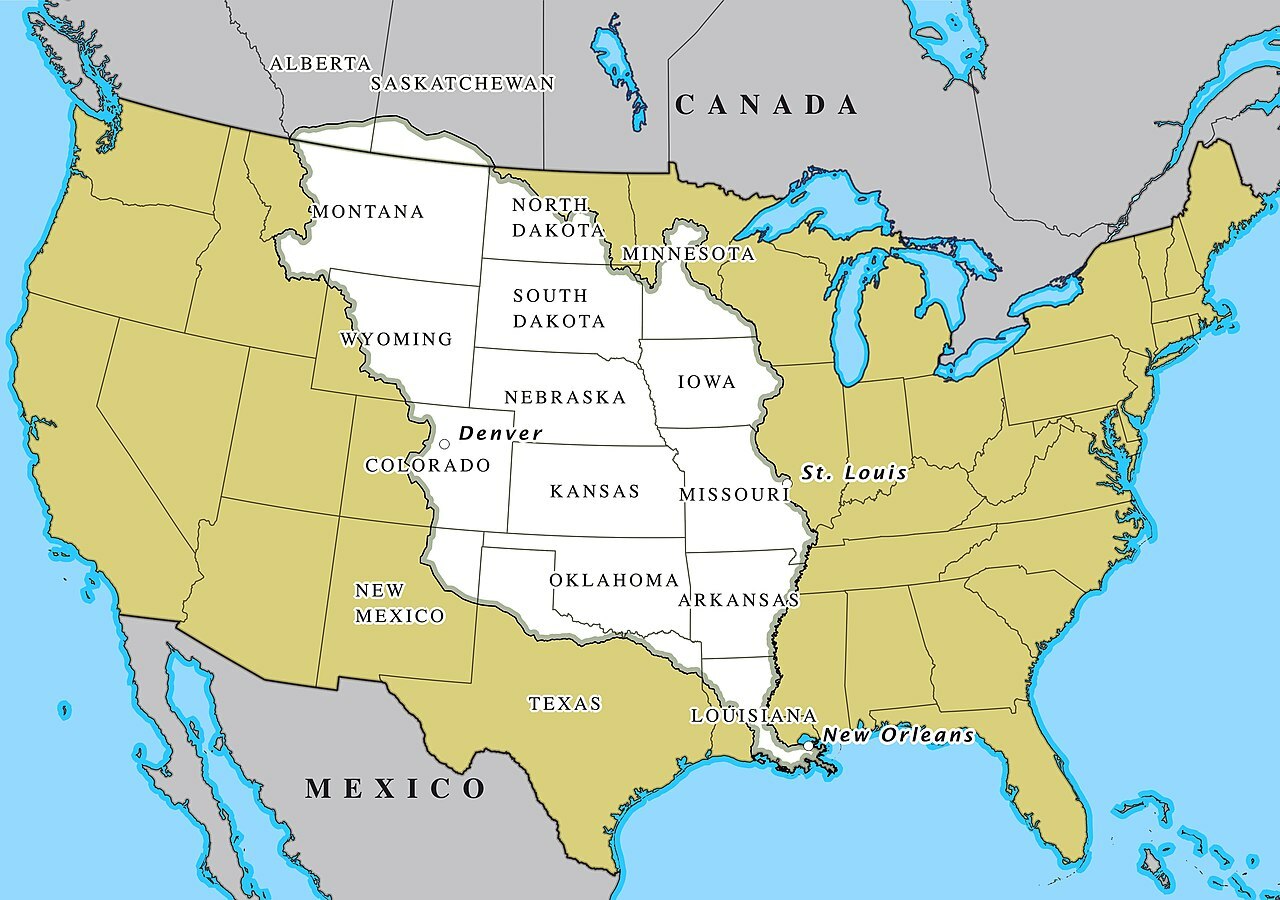
Луизианская покупка. Источник — https://ru.wikipedia.org/wiki/Луизианская_покупка#/media/Файл:Louisiana_Purchase.jpg
Все эти предположения часто делались на глазок и давали свои погрешности в виде огромных несуществующих континентов на картах, бессмысленных и опасных путешествий, которые стоили время, денег и человеческих жизней. В то же время это давало и свои дивиденды, несмотря на которые человечество продолжал на основе известных фактов предполагать, каким выглядит неизвестное пространство.
В этой серии статей мы поговорим об интерполяции, нахождении неизвестного на основании известного. Научимся делать ее тремя разными способами:
  • триангуляция Делоне (TIN интерполяция);
  • метод обратно взвешенных расстояний;
  • кригинг.
А в конце статьи мы сравним наши результаты с реальностью и определим, какой метод лучше.
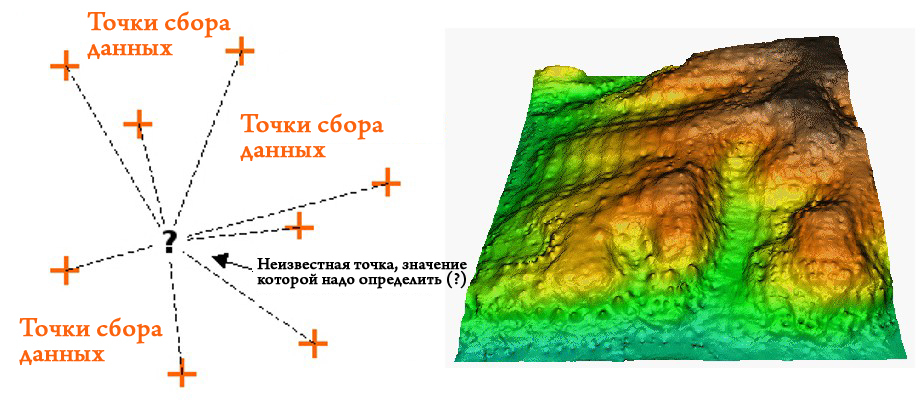
Суть интерполяции состоит в том, чтобы с помощью нескольких точек с известными значениями создать непрерывную поверхность, для каждой точки которой (или в нашем случае пикселя) имеется значение искомой переменной

О данных

Для интерполяции в QGIS нам необходим точечный слой со значениями, которые мы хотим проинтерполировать, чтобы получить растровый слой непрерывных значений. Для данного урока мы будем использовать значения высот, но вы можете использовать любые показатели, которые вам придут на ум и на жесткий диск, хоть температура, хоть гулябельность.
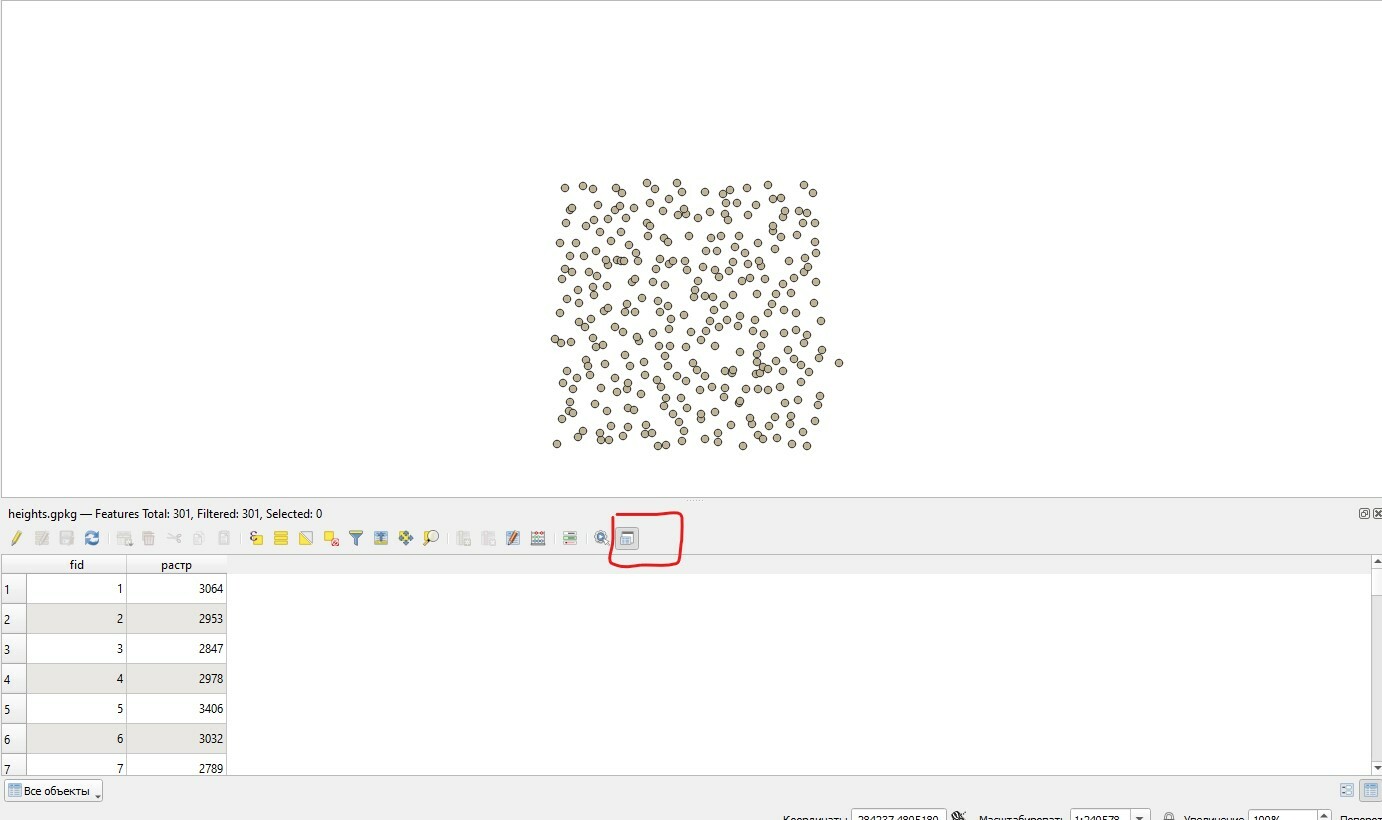
Так выглядит слой наших данных для интерполяции для примера работы алгоритмов. В слое на картинке 301 точка. На скрине я отметил, куда нажимать, чтобы таблица атрибутов слоя была не отдельным окном, а во встроенной панели, что часто бывает очень удобно.

Метод обратных взвешенных расстояний

Метод обратных взвешенных расстояний ОВР (Inverse Distance Weighted — IDW) уже был описан в нашем обзоре алгоритмов интерполяции, но вкратце напомним суть. В нем точкам придаются веса, от которых зависит, как сильно точка влияет на распространение значений в пространстве. Чем дальше от точки с известным значением, тем слабее ее влияние.
В QGIS есть множество вариантов интерполяции методом ОВР. Рассмотрим самый стандартный, который скрывается по пути Растр — Анализ — Интерполяция (обратно-взвешенное расстояние)
Тут мы видим очень много разных настроек, самое главное для нас — выбрать наш точечный слой, установить значения поля “вес” (чем больше, тем больше расстояние, на которое влияет точка) и в дополнительных параметрах выбрать в пункте “Значение Z из поля” поле, в котором у нас указаны исходные значения высот для интерполяции.
Получаем вот такой результат
Вот что получится, если в поле “вес” указать значение в два раза больше изначального — не 2, а 4.
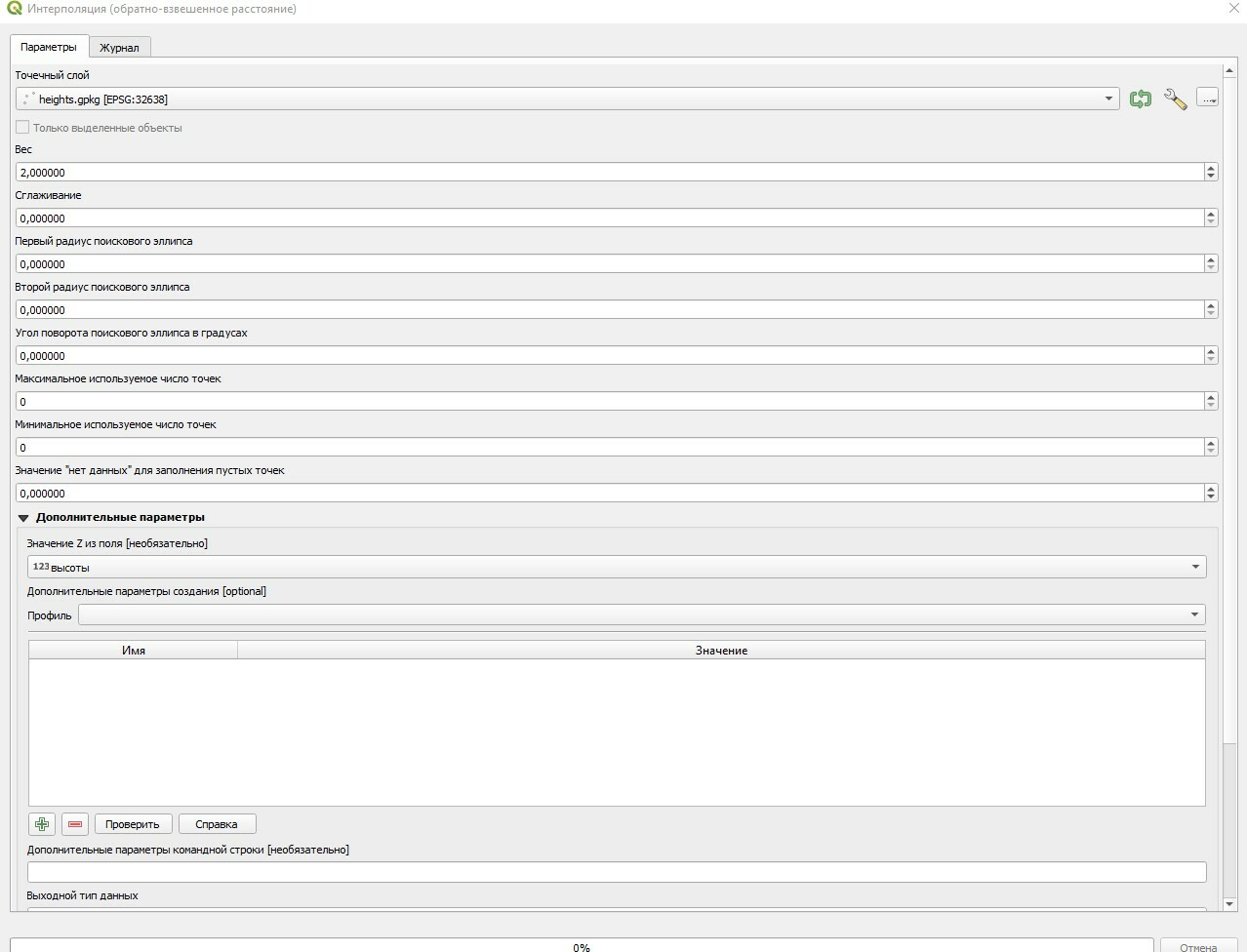
Метод содержит, конечно же, свои минусы (точки со значениями выделяются как пики и колодцы посреди равнины), но чем больше точек, с известными значениями, тем больше похоже на реальность.
А вот так, кстати, выглядит реальность. Разница довольно заметная, но что будет, если мы возьмем в сто раз больше точек?
Чтобы не дискредитировать метод ОВР, покажу вам, какой результат получится при стандартных настройках, если в слое расстояний будет не 301 точка, а 34176 точек с расстоянием 100 метров между ними.
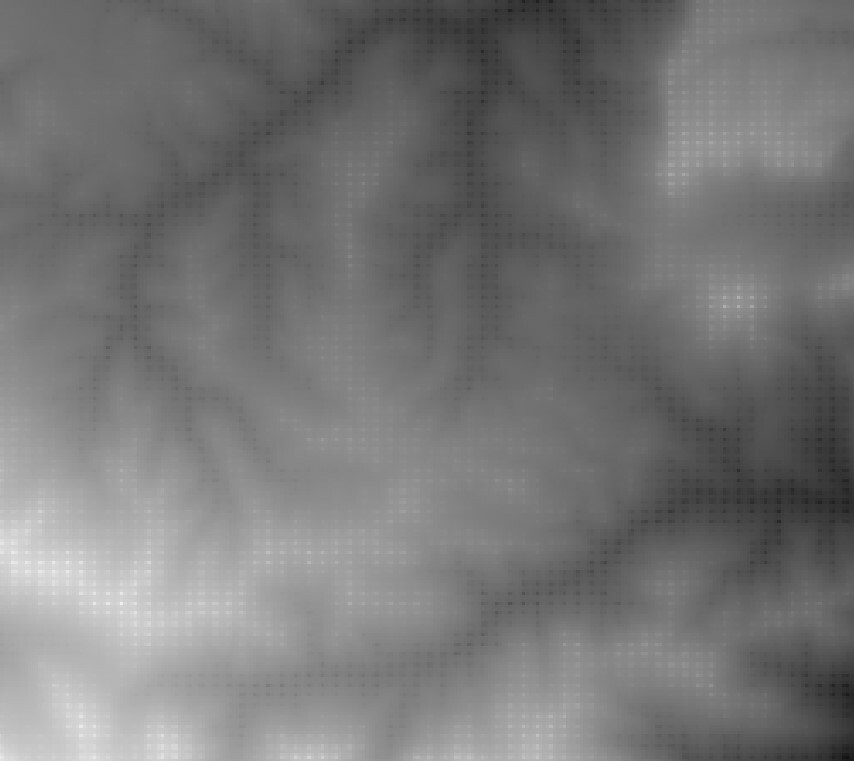
Вот так уже гораздо лучше, а при большей игре с различными настройками можно получить результат еще точнее. Главная сила метода ОВР — скорость. Все считается очень быстро, даже если счет точек идет на тысячи. Интерполяция кригингом в QGIS столько не осилит и отправит вас бесконечно смотреть на прогресс в 0%.

Триангуляция Делоне (TIN интерполяция)

Интерполяция методом триангуляции Делоне — популярный метод в ГИС. Алгоритм создает поверхность, состоящую из треугольников, формируемых ближайшими точками. Для этого вокруг точек, у которых есть значения, строятся окружности таким образом, чтобы в местах пересечений образовывались вершины треугольников, внутри которых нет вершин других треугольников.
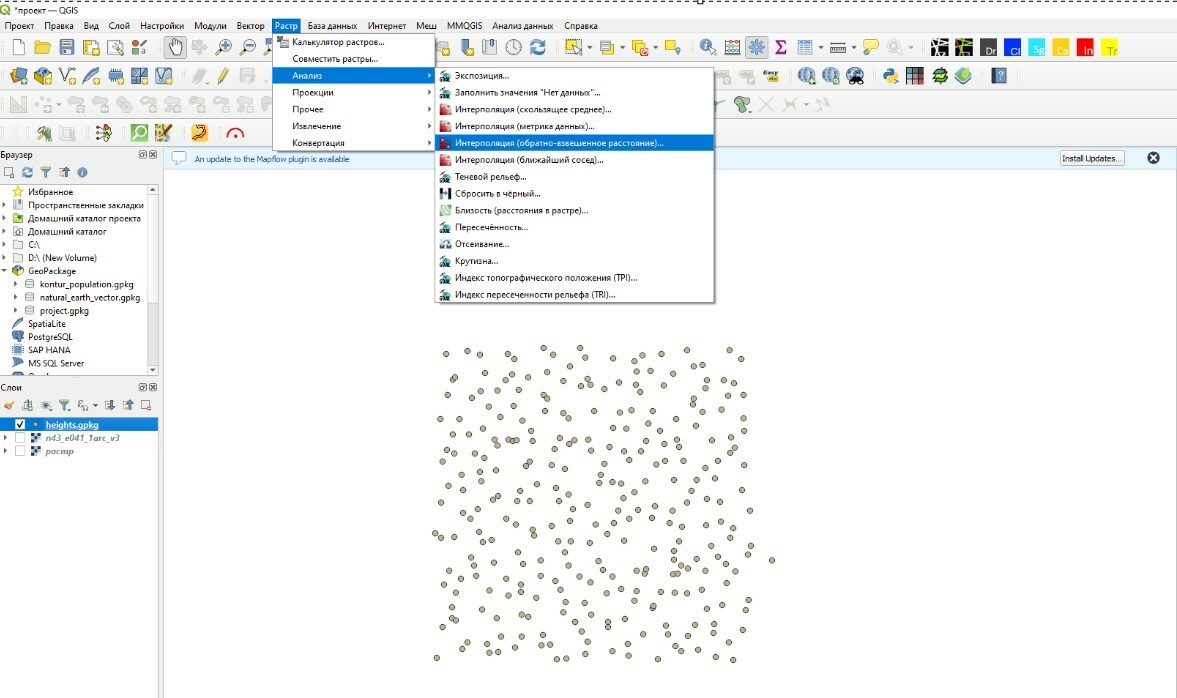
Триангуляция в QGIS прячется в боковой панели “Инструменты анализа”. Если у вас вдруг ее нет, то ее можно открыть, нажав вкладку “Анализ данных”, а затем выбрав “панель инструментов”. Можно также просто нажать Ctrl + Alt + T. Затем в поиске ищем инструмент “TIN интерполяция”.
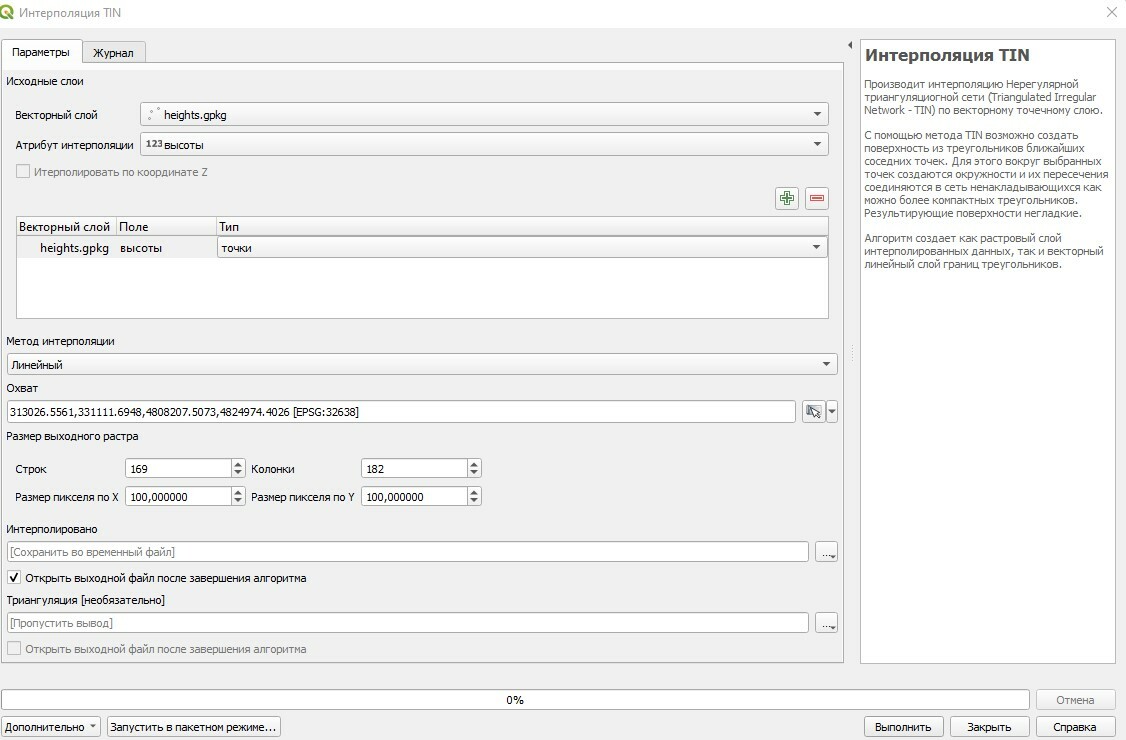
С триангуляцией Делоне нужно быть чуть внимательнее: устанавливаем слой и атрибут интерполяции как на скрине, выбираем метод интерполяции, охват и размер пикселя, после чего нажимаем "Выполнить".
Вот такой результат интерполяции получаем при использовании слоя с 301 точкой. Сильно угловатый растр — главная особенность триангуляции, черты местности слегка угадываются
Почему же TIN интерполяция? Т, понятно, триангуляция, откуда взялась I и N, и куда пропал Делоне?
TIN расшифровывается как Triangular Irregular Networks, что означает нерегулярные триангуляционные сети. То есть строится сетка треугольников, которая не выглядит, как регулярные квадратные сетки пикселей тех же растровых поверхностей. Триангуляция Делоне — это один из алгоритмов построения таких сетей, используемых для интерполяции значений, причем очень часто для интерполяции рельефа местности.
Если возьмем в 100 раз больше точек, то результат лучше, чем при методе ОВР, а скорость обработки совсем чуток дольше.
В этом уроке мы сравнили и научились использовать два метода интерполяции в QGIS. Главный плюс двух методов — быстрый расчет, но для приличной картинки нужно довольно большое количество данных при использовании любого из способов. В то же время даже при малых количествах данных получаются картинки немного похожие, но в разных стилях, что можно использовать в ситуациях, когда интересная подача важнее точности информации.
В следующем уроке мы рассмотрим интерполяцию в QGIS с помощью кригинга. Это более продвинутый метод, где больше заморочек и выше вероятность словить баг и вылетание QGIS, но, как по мне, результаты получаются лучше.

Источники:

Материал подготовил Александр Зуев