Как решается задача перехода из одной системы координат в другую? Разберемся с одним из стандартных вариантов – семипараметрическим преобразованием Гельмерта (или Хельмерта).
Преобразование из системы отсчета 1 в систему отсчета 2 можно описать через семь возможных параметров — три угла поворота вокруг каждой из осей (Rx, Ry, Rz), три компонента вектора сдвига (Δx, Δy, Δz) и масштабный коэффициент μ. Так и получается наиболее распространенное в геодезии семипараметрическое преобразование Гельмерта.
При преобразовании Гельмерта параллельные линии остаются параллельными, средняя точка отрезка прямой остается средней точкой, а все точки на прямой остаются на прямой.
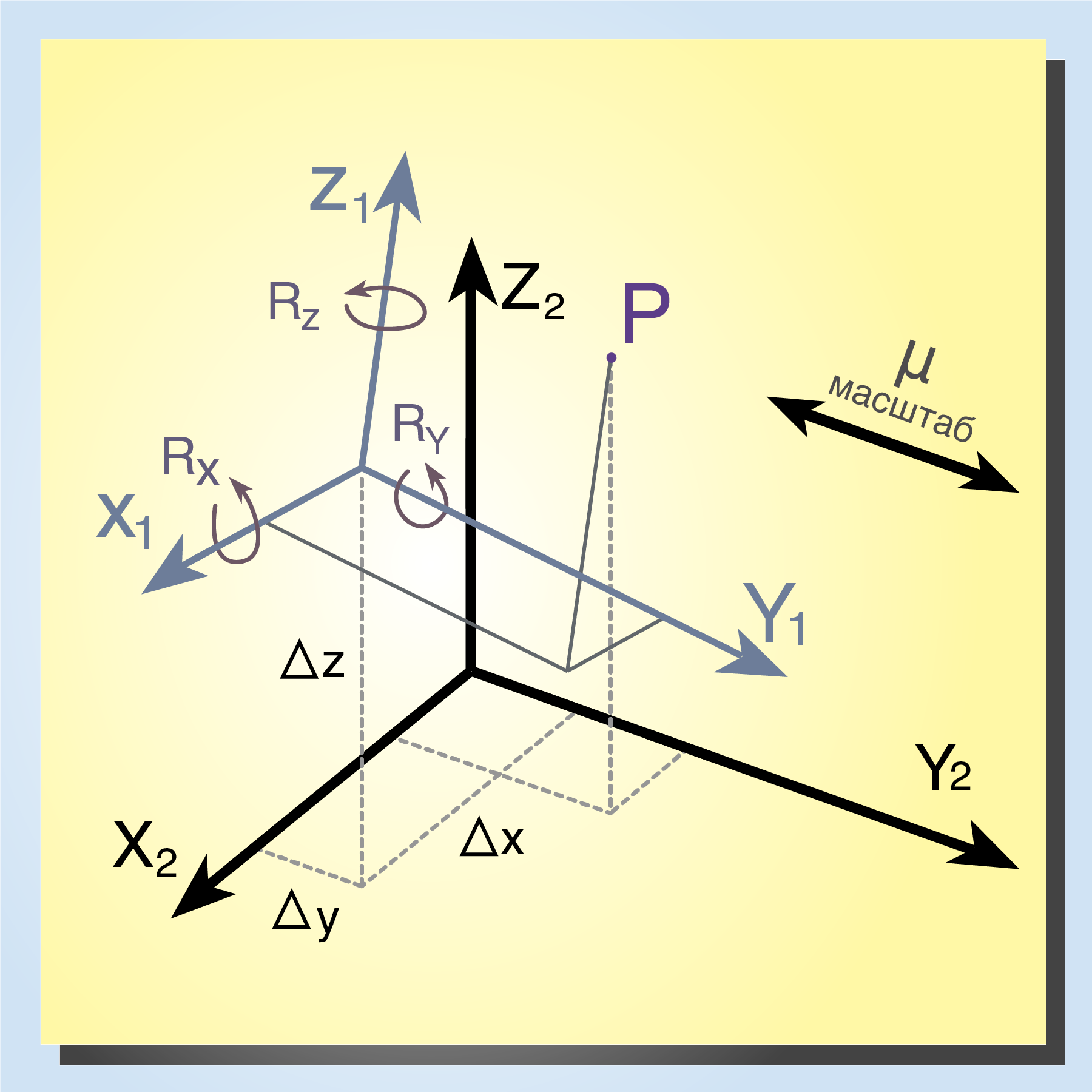
Семипараметрическое преобразование Гельмерта – это метод геометрического преобразования в трехмерном пространстве, которое часто используется в геодезии. В матричной форме:
Xt = C + μRX;
● X – изначальный вектор;
● Xt – конечный вектор;
● C – вектор трансляции со сдвигами осей;
● μ – масштабный коэффициент;
● R – матрица вращения, состоит из матриц Rx, Ry, Rz.
Это преобразование обычно выполняется в три этапа. Сначала исходная точка с геодезическими координатами преобразуется в трехмерные геоцентрические координаты (XYZ). Затем выполняется преобразование, после чего геоцентрические координаты преобразуются обратно в геодезические.
Пример применения – описание преобразования Гельмерта в программном обеспечении для перехода между системами координат PROJ.
Если параметры преобразования неизвестны, их можно вычислить с помощью точек, координаты которых известны до и после преобразования. Поскольку всего нужно определить семь параметров, необходимо знать как минимум координаты двух точек и одну координату третьей точки (например, Z-координату). Это дает систему с семью уравнениями и семью неизвестными, которую можно решить.
В некоторых задачах достаточно использовать преобразование с пятью параметрами, состоящее из трех сдвигов, только одного поворота вокруг оси Z и одного изменения масштаба. А если преобразование происходит в двумерном пространстве, потребуется всего четыре параметра (два сдвига, масштабирование, одно вращение). Их можно определить по двум известным точкам, а если имеется больше точек, то можно провести проверку.
У метода есть модификации – например, трансформация, учитывающая скорости изменения семи параметров во времени. Для их вычисления необходимо знать изменения координат опорных пунктов. Этот метод используется в высокоточных сетях, где производятся регулярные наблюдения, и для него нужно уже четырнадцать параметров — семь параметров метода Гельмерта и семь значений скоростей изменения каждого параметра.
Преобразование Гельмерта использует только один масштабный коэффициент, поэтому оно не подходит, например, для сравнения деформаций бумаги при сканировании старых планов и карт. В этих случаях предпочтительнее использовать более общее аффинное преобразование.
О точности преобразования
Хотя этот метод является математически точным, результат зависит от точности используемых параметров. На практике эти параметры вычисляются на основе как минимум трех известных точек. Однако их точность влияет на последующие параметры преобразования, поскольку эти точки будут содержать свои ошибки, к которым добавятся ошибки формул на разных этапах перехода. Итоговое преобразование будет лишь наилучшей оценкой из возможных.Источники:
● Методы трансформации геодезических и пространственных прямоугольных координат, их алгоритмы, параметры, точность – Г. Д. Курошев, А. А. Харунжий, Вестник СПбГУ, 2012.
● Helmert transformation.
● Helmert Datum Shift Methods.
Раз в две недели мы выбираем лучшие материалы блога про карты и геотехнологии, добавляем к ним полезные ссылки от команды и отправляем в нашей e-mail рассылке. Подписывайтесь, чтобы не пропустить новости от нас 💬
