Время прочтения: 6 минут

Оригинал: Caleb Jones на Unsplash
Введение
Картография – наука, в которой ответ на вопрос, какой длины тот или иной объект, может иметь множество самых разных значений, несмотря на простоту задания. Казалось бы, даже ребенок может взять линейку и измерить линию на карте, но все не так просто. На протяжении веков картографию окружает множество проблем, которые мешают идеально точно измерять размеры объектов, выявляемых с каждым годом все больше. Об одной из причин таких неточностей, называемой “парадокс береговой линии” пойдет речь в этой статье.
Эффект Ричардсона
Прародителем парадокса береговой линии считается, замеченный в 1951 году эффект Ричардсона.
Английский ученый с широким кругом интересов от математики до психологии, доктор Льюис Фрай Ричардсон был еще известен как убежденный пацифист. Некоторые из его работ были посвящены использованию математики для объяснения причин военных конфликтов с целью их предотвращения. В одной из своих статей доктор Ричардсон выдвинул теорию о том, что склонность войны между двумя нациями как-то связана с длиной и формой общей государственной границы между ними.
Для проверки своей теории английский математик собирал множество различных данных, формируя свою относительно репрезентативную статистическую выборку, пока не наткнулся на занимательный факт. Протяженность границ в разных источниках между Испанией и Португалией варьировалась от 987 до 1214 километров, а между Бельгией и Нидерландами – от 380 до 449 километров.
Причина такого различия в измерениях кроется в генерализации карт. Карта – образно-знаковая модель земной поверхности и объектов на ней. Точность и детальность отображения объекта зависит от масштаба карты и степени обобщения элементов. В докомпьютерные времена карты рисовались на бумаге для того, чтобы люди работали с ними на бумаге, используя такие инструменты, как циркули, кульвиметры, логарифмические линейки и прочие измерительные приборы.

Измерения на картах зависят от нижнего предела длины географически значимых объектов (его обозначают еще как G), обычно это расстояние, которое на карте определенного масштаба докомпьютерной эпохи имело длину 1 мм, так как 1 мм – приблизительно наименьший отрезок, который на бумажной карте можно, во-первых, точно нарисовать, а во вторых, точно измерить. С развитием компьютерных технологий такой нижний предел длины географически значимых объектов встречается все реже, так как скорость обработки информации и требуемая точность ее воспроизведения стали приоритетнее возможностей работы с бумагой.
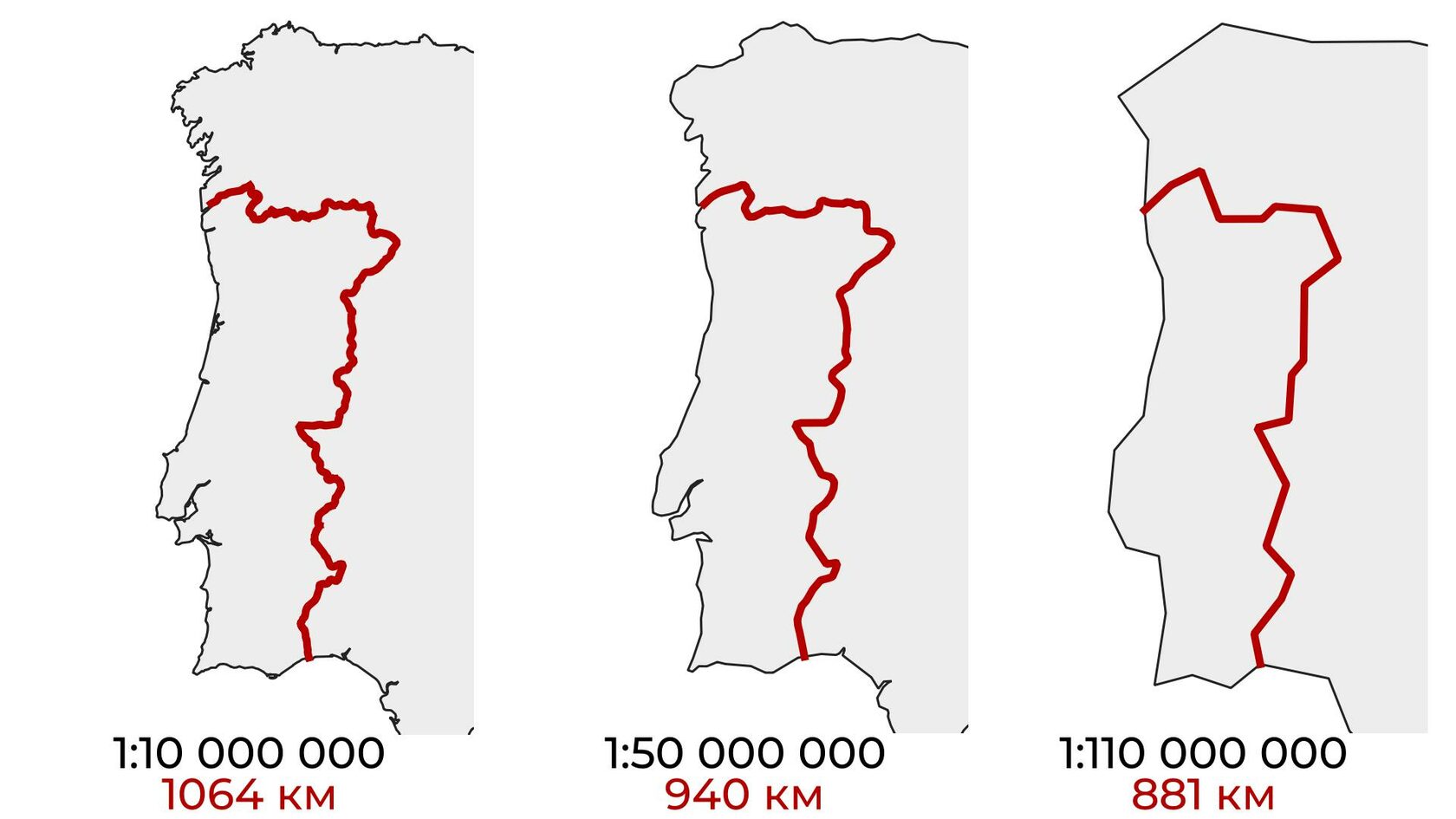
Изучая информацию о длине границ Испании и Португалии, доктор Ричардсон выяснил, что протяженность границ в разных источниках измерялась на картах разного масштаба. Чем больше расстояние 1 мм на карте в реальности, тем большее количество деталей упускается из виду: объекты обобщаются и выпрямляются, игнорируя изгибы.
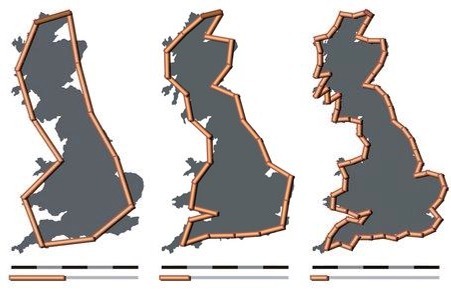
Исследуя данный эффект, доктор Ричардсон заметил, что чем меньше длина отрезка на карте в действительности, тем больше становится длина объекта, состоящего из множества таких объектов. Английский математик предполагал, что в какой-то момент длина объекта перестанет расти и придет к истинному значению, подобно тому, как периметр многоугольника, вписанного в окружность, тем ближе к длине окружности, тем больше у него сторон. Собственно это и есть основное отличие эффекта Ричардсона от парадокса береговой линии – эффект Ричардсона предполагает, что даже береговая линия Великобритании с множеством мысов и заливов – это кривая, которую рано или поздно можно спрямить.
Парадокс береговой линии
В своем исследовании доктор Ричардсон задумался о том, что береговая полоса – еще более искривленная линия, чем государственные границы, но все же точность ее измерения его не сильно интересовала. Для него береговая линия была лишь отметкой, от которой отсчитываются границы, отделяющие территориальные воды одного государства от территориальных вод другого или международных вод.
Спустя более десяти лет после открытия эффекта Ричардсона другой ученый, Бенуа Мандельброт, более плотно занялся вопросом точности измерения длин кривых линий, что вскоре привело к созданию фрактальной геометрии, да и в принципе к возникновению слова "фрактал" в научном поле.
Во фрактальной геометрии как раз и кроется определение парадокса береговой линии. Статью Мандельброта “Какова протяженность побережья Британии? Статистическая самоподобие и дробная размерность” считают истоком фрактальной геометрии за 10 лет до того, как Бенуа Мандельброт самолично введет понятие фрактал.
фрактал – множество, обладающее свойством самоподобия (объект, в точности или приближенно совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей)
Мандельброт описывает формы морского побережья как сложные кривые, каждую часть которых можно назвать уменьшенным изображением целого. Это свойство он тогда назвал “статическим самоподобием”. Более того, в своей работе он вообще предполагает, что понятие “длина” для них не имеет смысла, так как географические кривые из-за различных масштабов представления на разных картах с разными целями находятся в суперпозиции, то есть одновременно могут иметь широкий разброс характерных размеров. Например, измеряя побережье Великобритании условными линейками 50 и 100 км, мы получим протяженность побережья соответственно около 3500 и 2800 км.
Самоподобие береговой линии выражено чередованием заливов и мысов. Чем точнее мы описываем побережье, тем больше заливов и мысов мы можем выделить, и, более того, сами заливы и мысы содержат внутри себя другие заливы и мысы. Таким образом мы можем бесконечно точно описывать береговую линию чего угодно. Чем точнее мы будем ее описывать, тем больше будет ее протяженность, и когда в конце концов минимальное расстояние нашей условной линейки будет стремиться к нулю, общая длина измеряемой береговой линии будет стремиться к бесконечности.
Парадокс береговой линии – это теоретическая модель, которая говорит нам о невозможности и даже бессмысленности в выполнении задачи по точному измерению береговой линии, так как она представлена виде бесконечного количества самоподобных форм. Государственные же границы далеко не всегда обладают такими свойствами, ведь они проходят не только по границам рек и морей, а частенько просто проведены прямыми линиями вдоль меридианов и параллелей.
Практические выводы
Парадокс береговой линии – теоретическая концепция, и за истину все же принимать ее не стоит, если говорить с практической точки зрения. В реальности нет никакой необходимости измерять береговую полосу до песчинки или до атома, к тому же с каждым приливом и отливом, с каждым ударом морской волны о песчаный пляж береговая линия подвергается эрозии, и задача по идеально точному ее измерению представляет собой сизифов труд.
Но что же тогда дает на практике нам парадокс береговой линии? Еще один занимательный факт? Повод придумать шутку, про невозможность строительства стены от мигрантов вдоль границы США проходящей по реке Рио-Гранде, так как стоимость строительства будет стоить бесконечно много денег?
На мой взгляд, парадокс береговой линии – это лишний повод держать в голове тот факт, что в работах на стыке географии и математики нужно искать баланс между точностью и целесообразностью. В попытках идеально точно изобразить объект можно обнаружить, что либо на карте не видны все эти усилия, либо ни одна ЭВМ в мире не способна прогрузить ваше творение быстрее среднестатистического тиктока, что для пользователей веб-карт имеет существенное значение.
Работа “Какова протяженность побережья Британии? Статистическая самоподобие и дробная размерность” была не первой статьей Бенуа Мандельброта, связанной с фракталами. В одной из своих аннотаций ученый пишет, что до этой работы его предыдущие выступления на тему “фрактальной размерности” встречали слышимое неодобрение, а его работы считались бесполезными для науки. Находка в виде эффекта Ричардсона стала настоящим “Троянским конем” в мире сложной математики через легко объяснимые явления, которые можно встретить, сравнив между собой две карты разных масштабов.

Та самая шутка (источник – SMBC)
Источники:
- http://li.mit.edu/Stuff/CNSE/Paper/Mandelbrot67Science.pdf – How long is the coast of Britain? Statistical self-similarity and fractional dimension
- https://users.math.yale.edu/~bbm3/web_pdfs/howLongIsTheCoastOfBritain.pdf – How long is the coast of Britain? Statistical self-similarity and fractional dimension (с аннотациями автора)
- https://www.futilitycloset.com/2013/12/02/the-richardson-effect/– про Эффект Ричардсона
