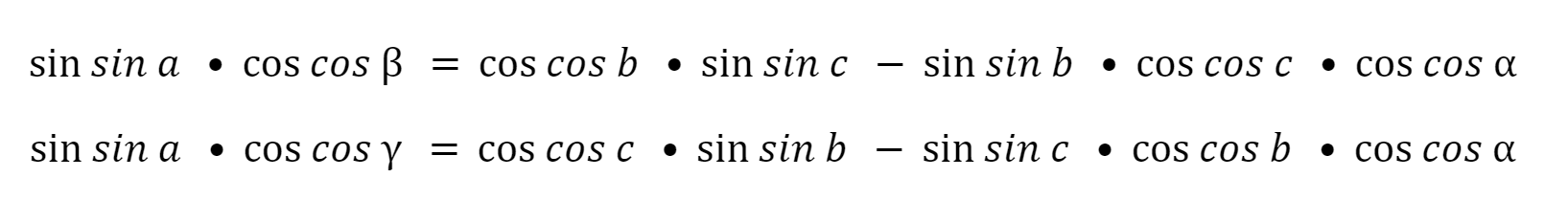В 1956 году Сэмюел Шентон возродил Международное общество плоской Земли. Это общество стремится доказать, что Земля – плоская. По мнению его членов, Земля – плоский диск 40 000 километров в диаметре. Северный полюс – центр диска. Южного полюса не существует, а Антарктика является ледяной стеной, опоясывающей мир.
Если вы сторонник плоской Земли, то это статья не для вас, потому что она посвящена сферической геометрии. Эта научная дисциплина занимается изучением геометрических фигур на сфере. Ее возникновение и развитие неразрывно связано с доказательством шарообразности Земли и других небесных тел.
Простейших практических задач, которые решала сферическая геометрия, было две. Первая – определение расстояния между точками (например, между городами или между звездами). Вторая – определение направления и угла до объекта. Так, сферической теоремой косинусов пользовались мусульмане, когда искали направление на Мекку. Для этого им нужно было знать координаты своего местоположения.
Сферическая геометрия – прежде всего база, на основе которой, учитывая конкретные задачи, развиваются остальные науки. Сегодня эти знания применяют в астрономии, космической геодезии, картографии, сфероидической геодезии, навигации.
Основные положения
Многие положения для геометрии на сфере аналогичны геометрии на плоскости, но есть и различия. Перечислим некоторые из основных положений:
- Прямая на сфере всегда замкнута.
- В сферической геометрии не существует параллельности.
- Две сферические прямые пересекаются в двух диаметрально противоположных точках.
- Все углы в сферическом треугольнике могут быть прямыми.
- Любая плоскость, которая пересекает сферу, образует в сечении окружность.
- Углы на сфере определяются двугранными углами, а сферические расстояния измеряются в угловой мере. Для перехода к линейной мере необходимо знать радиус сферы.
Термины сферической геометрии
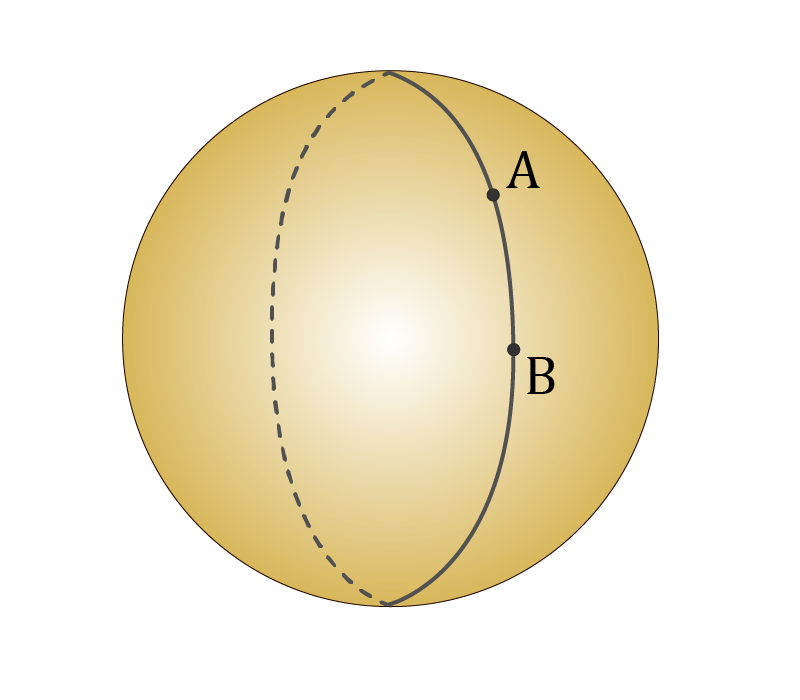
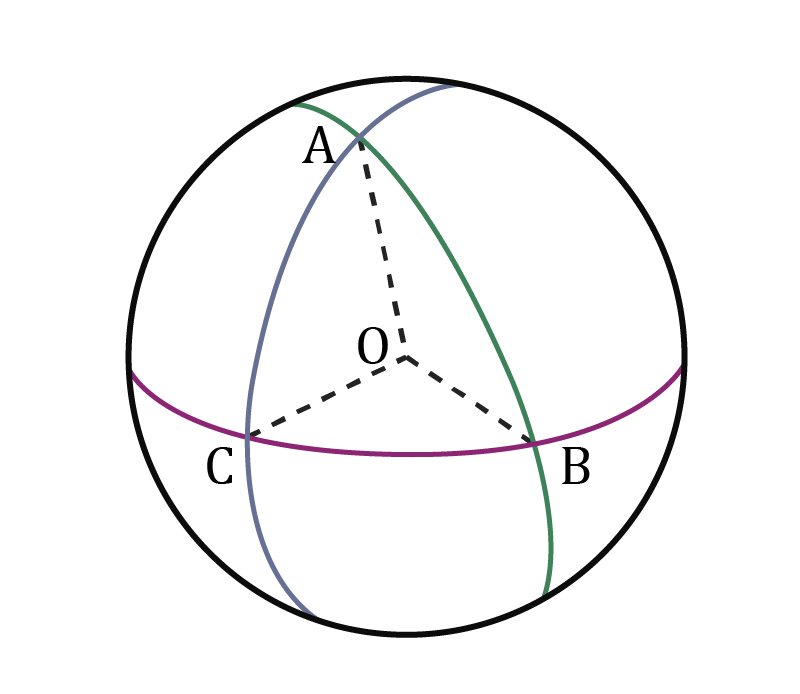
Сфера, дуга, большой круг, сферический отрезок, сферический треугольник, геодезическая линия, двуугольник, сферический избыток, треугольник Лежандра, прямосторонний сферический треугольник, прямоугольный треугольник, сферическая система координат.Сфера – геометрическое место точек, равноудаленных от некоторой заданной точки – центра.


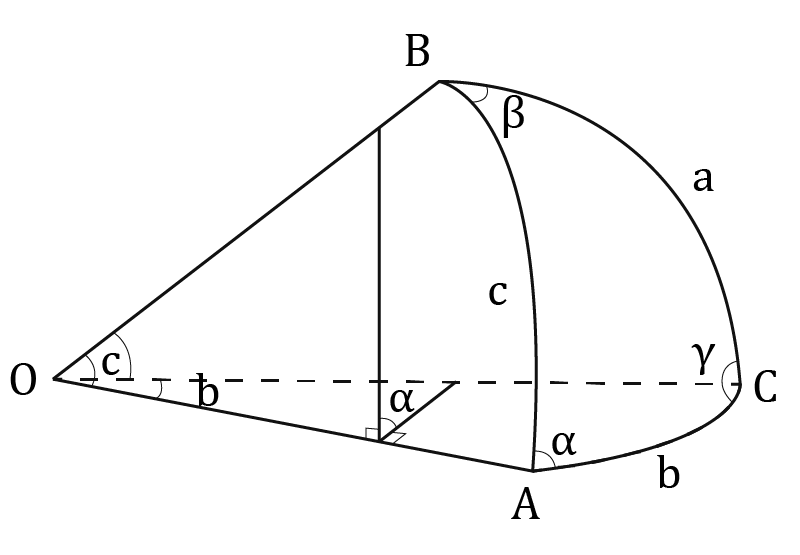
Формулы сферической тригонометрии
Теорема синусов
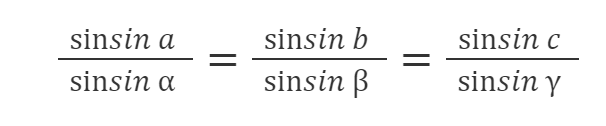
Синусы сторон сферического треугольника пропорциональны синусам противолежащих углов.
Теорема косинусов углов
Косинус угла сферического треугольника равен произведению косинусов других углов с обратным знаком, сложенному с произведением их же синусов на косинус стороны между ними.
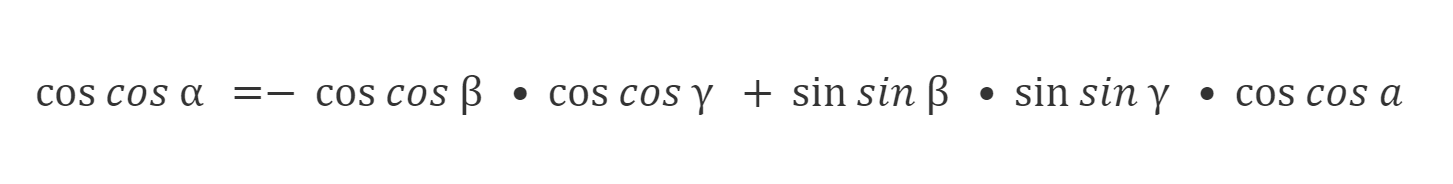
Теорема косинусов сторон
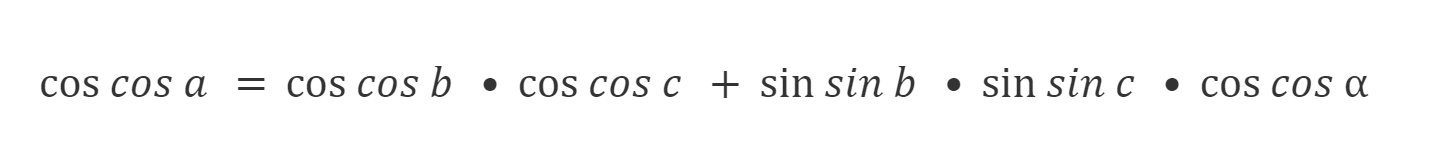
Косинус стороны сферического треугольника равен произведению косинусов двух других, сложенному с произведением их же синусов на косинус угла между ними.
Теорема о пяти элементах
Произведение синуса стороны на косинус прилежащего угла равно произведению косинуса противолежащей углу стороны на синус третьей стороны, вычесть произведение синуса противолежащей стороны на косинус третьей стороны и на косинус угла между ними.