Время прочтения: 6 минут
Введение
Привязка растров — один из самых часто используемых ГИС-инструментов. Взять допотопную карту времен, когда персональных компьютеров еще не было, либо векторные слои которой давно канули в лету, чтобы выжать из нее все информационные соки, не раз спасало из передряг пользователей ГИС. Возможно, вы даже уже пользовались этим инструментом не раз, но вот знаете ли вы, чем отличается линейная трансформация растра при его привязке от полиномиальной 3 порядка? И что еще за методы передискретизации? Ответы на эти вопросы в этой статье!
Привязка растров - база
Привязка растров или georeferencing - это процесс в результате которого карта в формате jpg или png обретает координаты, которые превращают ее из простого набора пикселей в набор пикселей с географическими координатами.
Вот обычная картинка — геологическая карта Крыма под редакцией Фохта (источник - https://ar.culture.ru/ru/subject/geologicheskaya-karta-kryma)
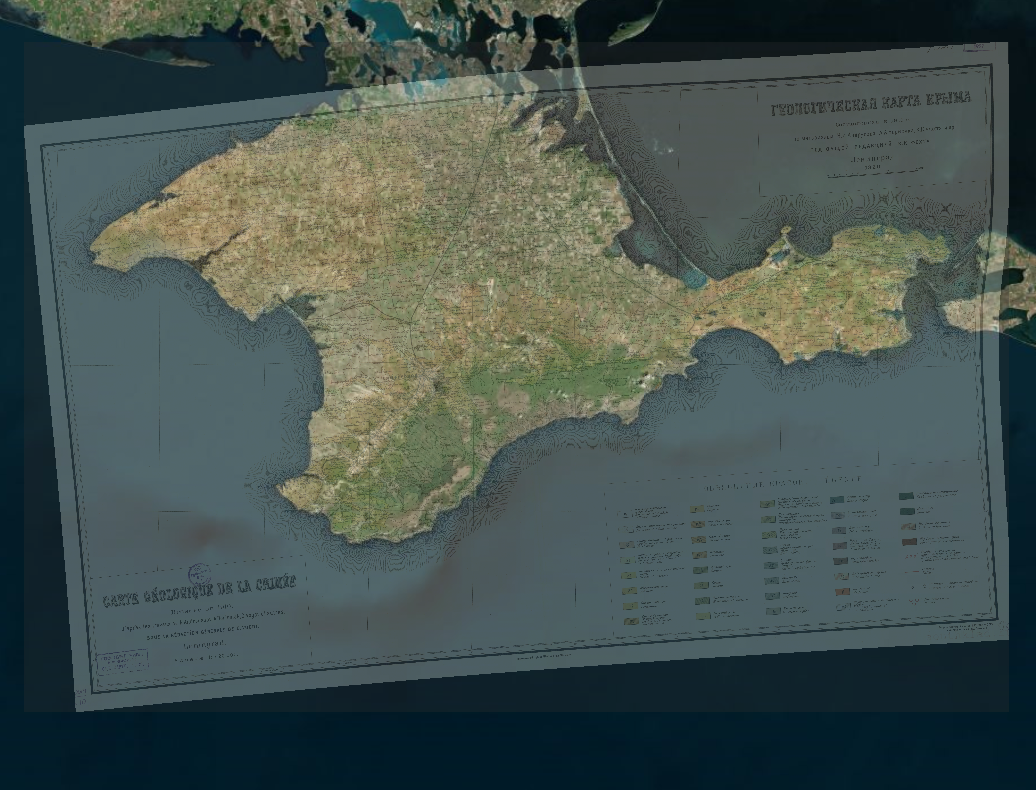
А вот уже привязанная карта — картинка искажена, но имеет реальные координаты, ее формат — GeoTIFF, и она прекрасно совмещается с современными картами, например, со спутниковым снимком от BING
Привязать растр можно в абсолютно любой ГИС-программе, принцип везде одинаковый и сводится к тому, что нужно совместить точки на растровой картинке с точками, у которых есть координаты. С точки зрения программы, происходит поиск закономерностей с тем, как “координаты” картинки, измеряемые в пикселях, соответствуют координатам карты, измеряемым в градусах или метрах.
Под капотом привязки растров для сопоставления картинки с координатами происходит 2 процесса: трансформация растра и ресэмплинг (передискретизация). Понимание этих процессов поможет вам быстрее и эффективнее привязывать растры, более глубоко понимая суть процессов.
Если вы в целом знаете основы, но всегда используете старый-добрый линейный алгоритм трансформации растра, потому что он работает, то дайте нам знать об этом поставив эмодзи-кита в реакции к посту с ссылкой на эту статью в телеграм.
Алгоритмы трансформации растра
Алгоритм трансформации растра – методика преобразования растра, выраженная в формуле, которую нам знать необязательно, с помощью которого программа крутит, растягивает, сжимает нашу картинку, чтобы подогнать ее под имеющиеся географические координаты. Каждый алгоритм имеет свои требования и свои свойства, какие-то могут только слегка поворачивать нашу картинку, а какие-то могут растянуть так, что от прямоугольной формы ничего не останется.
Выбор алгоритма трансформации растра (в QGIS называется тип трансформации) — первая по списку и фактически самая важная настройка при привязке растра в любой ГИС.

Эта картинка поможет вам лучше понять, как работают алгоритмы трансформации растра (источник - https://gis.stackexchange.com/questions/367659/differences-between-different-georeferencing-transformation-algorithms-in-qgis)
Линейная трансформация (Linear)
Самый простой алгоритм трансформации. От вас требуется сопоставить хотя бы 2 точки между картинкой и координатами местности. Алгоритм перемещает изображение в указанное место, может увеличивать его или уменьшать, на этом все возможные преобразования заканчиваются, даже вращать растр алгоритм не умеет.
Линейная трансформация отлично подходит для карт в хорошем качестве, где точно известна система координат.
Точки, которые создаются для сопоставления картинки с координатами местности называются ground control points (GCP, далее по тексту я буду использовать термин “контрольные точки”), ГИС-программы позволяют их сохранять отдельно для файлов привязки, чтобы их можно было использовать еще раз, например, если захочется попробовать иной алгоритм трансформации, для лучшей привязки растра.
Трансформация Гельмерта (Helmert)
Трансформация Гельмерта — еще один алгоритм, который быстро и эффективно работает с хорошими картами, где хотя бы примерно понятно, какая проекция использовалась для подготовки карты. В отличии от линейной трансформации изображение может быть повернуто, для сопоставления картинки и координат карты. Для работы алгоритма также требуется 2 контрольные точки.
Полиномиальная трансформация 1 порядка (Polynomial 1)
Полиномиальная трансформация 1 порядка может не просто масштабировать картинку и поворачивать, как предыдущие методы, но и способна сдвигать точки, при необходимости, превращая нашу прямоугольную картинку в параллелограмм, сохраняя параллельность линий. Для работы алгоритма потребуется уже как минимум 3 контрольные точки. Прекрасно работает в тех же ситуациях, что и предыдущие 2 алгоритма трансформации, а зачастую дает даже более точные результаты.
Полиномиальная трансформация 2, 3 и более порядков (Polynomial 2, Polynominal 3 …)
Эти алгоритмы используют в своем арсенале еще больше инструментов для сопоставления картинки с координатами на местности. Помимо вращения, смещения и масштабирования может растягивать и сжимать картинки в разной степени в разных ее частях. Чем больше степень полиномиальной трансформации (в ГИС обычно нет возможности стандартными средствами проводить полиномиальные трансформации выше 3 порядка), тем сильнее в разных частях изображения происходит его деформация для сопоставления картинки и географических координат. Для использования полиномиальной трансформации 2 порядка нужно уже как минимум 6 контрольных точек, для 3 порядка — не менее 10. Такой способ часто используют для привязки сфотографированных карт с закругленными краями.
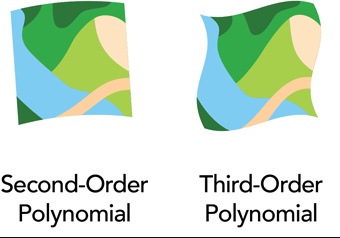
Сравнение полиномиальных трансформаций 2 и 3 порядков, чем больше порядок, тем сильнее происходит искривление линий. Такой способ подходит для самых тяжелых случаев, например, для карт, которые делались вообще без какой-либо проекции (Источник - https://www.esri.com/about/newsroom/arcuser/understanding-raster-georeferencing/)
Проективная трансформация (Projective)
Этот метод очень похож на полиномиальную трансформацию 1 порядка. Вращает и растягивает координаты, сохраняя прямые линии прямыми, но вот параллельность не сохраняется. Для использования алгоритма нужно не менее 4 контрольных точек. Такой тип преобразования часто используют для аэрофотоснимков или карт, которые хорошо сфотографировали (именно сфотографировали, а не отсканировали), но сделали это под углом. В общем, отличный способ привязать карту, которую вы сфотографировали в музее.
Тонкостенный сплайн (Thin Plate Spline - TPS)
Алгоритм представляет собой комбинацию полиномиальных методов. Для привязки алгоритм создает несколько формул для разных мест карты, чтобы лучше ее сопоставить с местностью. Для использования нужно минимум 10 контрольных точек, но обычно для адекватного результата нужно больше. Применяют такой алгоритм для поврежденных, либо просто очевидно неточных карт.
Ресемплинг или передискретизация
В процессе привязки растров, происходит растягивание или увеличение изображения, в процессе чего разрешение изображения может меняться. Этот процесс как раз и называется рэсэмплингом (также используется термин передискретизация). Тема довольно обширная и заслуживает отдельной небольшой статьи.
В случае с привязкой растра нужно знать о ресемплинге следующее — при трансформации растра, растягивая наш растр или сжимая, для корректного сопоставления с местностью мы меняем разрешение нашей изначальной картинки, условно, до привязки расстояние между городами было 100 пикселей, а после привязки и сохранения изображения в таком же качестве стало 120 пикселей.
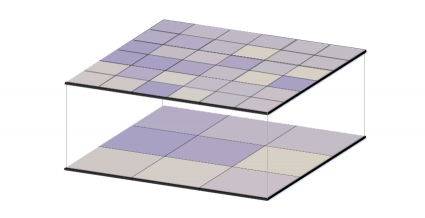
Фактически, ресемплинг (передискретизация) — процесс, в котором мы меняем количество пикселей, которое нужно для отображения каких-либо объектов или данных (источник - https://gisgeography.com/raster-resampling/)
Тип использования метода передискретизации зависит от алгоритма трансформации. Если ваше изображение существенно не изменяется и нет никаких неравномерных преобразований, то можно спокойно выбирать метод “Ближайший сосед” (nearest neighbor). Практически всегда хорошо работает для линейной трансформации, полиномиальной 1 степени и Гельмерта, для остальных лучше использовать кубическую передискретизацию, которая, на мой взгляд, вообще хорошо подходит к любому алгоритму привязки растра.
Использованная литература и источники дополнительной информации
Материал подготовил Александр Зуев
